Behnam Sadeghi has published this paper in the Iranian Journal of Earth Sciences. In this research, he has developed an algorithm to down-scale the maps, to reduce the simulation time and the required memory, but to keep the same geostatistical performance and accuracy. This model strongly helps with huge and time-consuming simulations.
Abstract
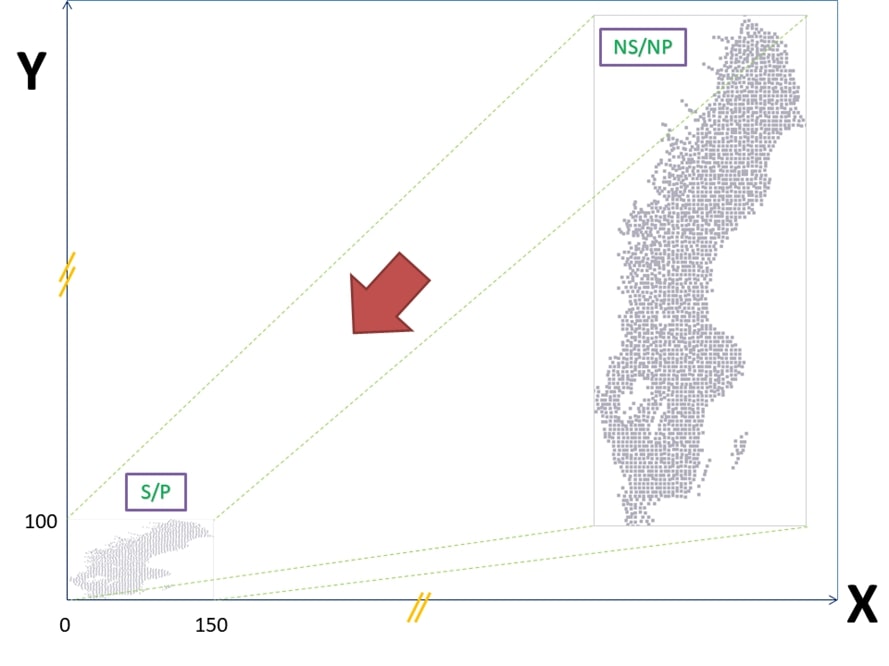
In geochemical anomaly classification, different mathematical-statistical models have been applied. The final classified map provides only one scenario. This model is not certain enough since every model provides several thresholds which are almost different from each other meaning dissimilarity and spatial uncertainty of the classified maps. Spatial uncertainty of the models could be quantified considering the difference between the associated geochemical scenarios simulated (called: ‘realizations’) by geostatistical simulation (GS) methods. However, the main problem with GS methods is that these methods are significantly time-consuming, and CPU- and memory-demanding. To improve such problems, in this research, the method of “scaling and projecting sample-locations (SPS)” is developed. Based on the SPS theory, first of all, the whole sample-locations were projected (centralized) and scaled into a box coordinated between (0,0) to (150,0) and (0,0) to (0,100), for example (they can be equal though), with the cell-size of 1 m2. Therefore, the time consumed and the memory demanded to generate a large number of realizations, for example, 1000 realizations based on the non-scaled/non-projected (NS/NP) and scaled/projected (S/P) sample locations per case-study were quantified. In this study, the turning bands simulation (TBSIM) were applied to geochemical datasets of three different case studies to take the area scales, regularity/irregularity and density of the samples into account. The comparison between NS/NP and S/P results statistically demonstrated the same results, however, the process and outputs of the S/P samples took a significantly shorter time and consumed a remarkably lower computer-memory. Therefore, experts are able to easily run this algorithm using any normal computer.
Full link to this paper is:
http://ijes.mshdiau.ac.ir/article_680583.html
![]()

